[Puzzle] Instant Insanity

In this section I would like to try something different in proposing a puzzle to you all. In the game of Instant Insanity, where 4 cubes are used, each side of a cube is painted one of the colours red, green, white or blue. For example in the following way:

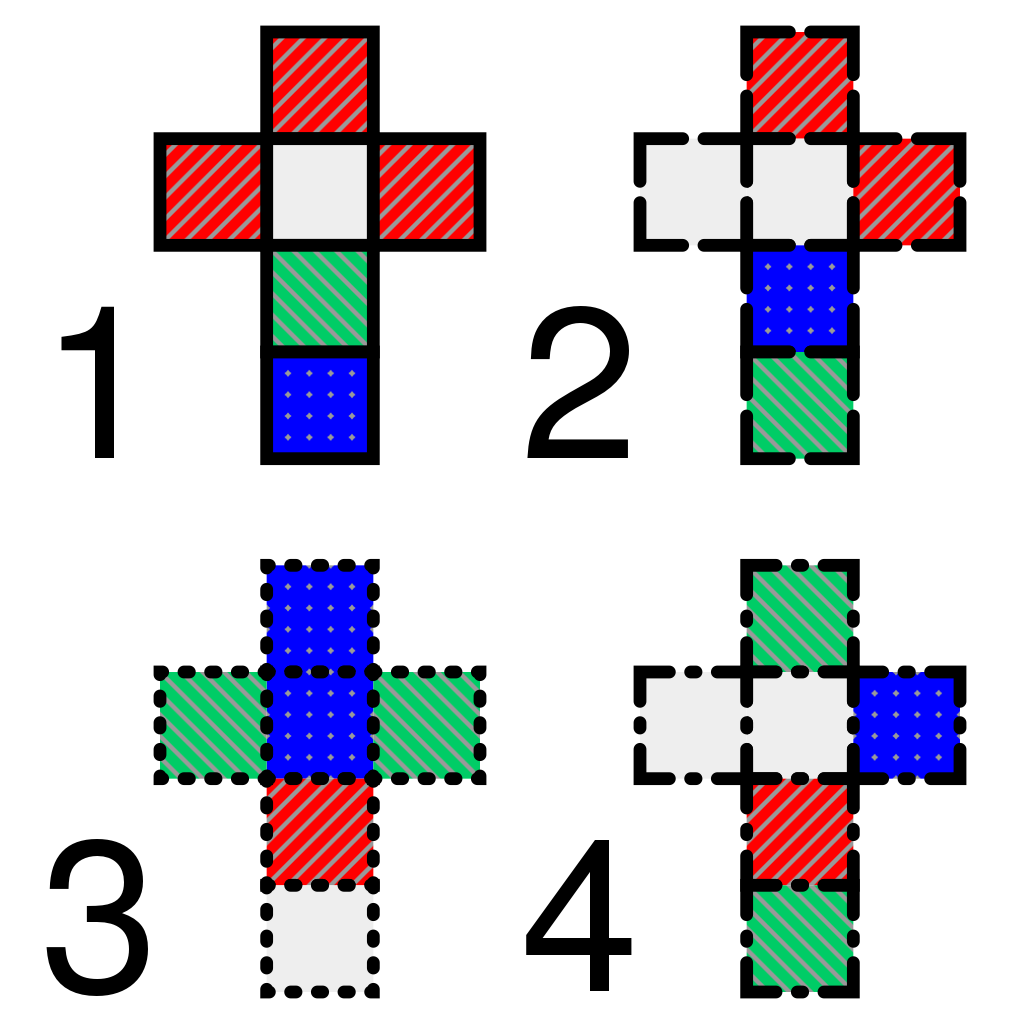
Depending on how the cubes are coloured, there may or may not exist a solution. A solution being that the cubes are placed in a  column (or row) of four such that all four (different) colours appear on each of the four sides of the column. This is an example solution:

One observation, which is useful in solving the puzzle, is that with three pairs of opposite faces there will be at most three ways to place cube 1 (and any other cube). This is because it makes no difference whether we place the green face on the table or the opposite red face on the table: the middle layer will stay the same.

We can represent this information in a graph, where each colour is a node and an edge is drawn between two colours if they appear on opposite sides of any of cubes 1-4. In addition, the edge is labelled with the number of the cube on which these opposite colour sides appear. For our initial colouring, this gives the following graph:

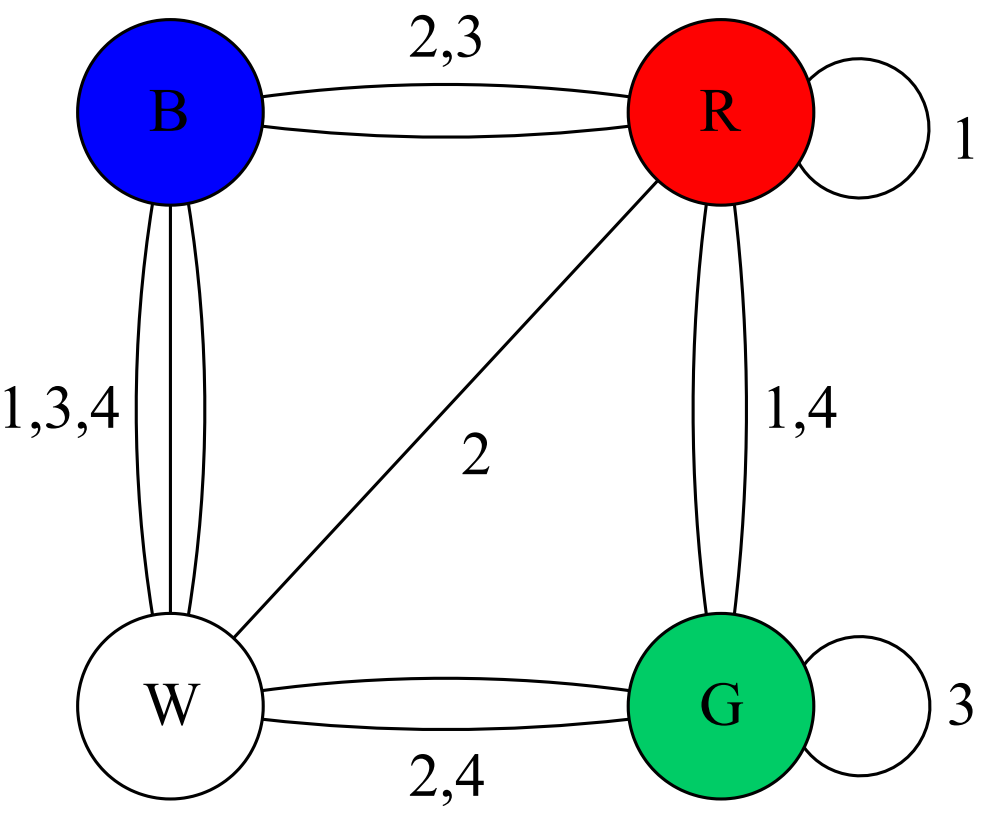
Suppose we had an arrangement of cubes that was a solution. Then, from each cube, pick the edge representing the colours facing front and back on that cube. These four edges are a subgraph of our original graph. Furthermore, to form a solution to instant insanity, each colour appears once on the front face and once on the back (there is another subgraph for the left and right faces of the column). This means that for our subgraph, each vertex has degree two.

We can get another subgraph satisfying these two properties for the left and right faces of the pillar. Furthermore, these two subgraphs cannot have any edges in common.

So, to find a solution to instant insanity, we must find a pair of subgraphs S1, S2 such that:

• Each subgraph has one edge with each label 1,2,3,4
• Every vertex of a subgraph has degree 2
• No edge of the original graph is used in both S1 and S2
  Can you find an arrangement of cubes 1,2,3,4 such that the example solution is satisfied?

Participating

Solutions can be sent to iovivat@inter-actief.net. We will give away two cinema vouchers to those who did send in a correct solution.

We will publish the solution to this puzzle next edition.