Pensions, Portfolios, and Pareto

They wield vast sums of money that can change the economic climate of a small country in one fell swoop, take your money each month while you do not even complain, and you have probably never given them a second thought. No, this article is not about the lizard people, it is about pension funds!

In the massive oceans of 21st-century finance, pension funds are the blue whales. Like their plankton-feeding counterparts, these gentle giants swim around our financial oceans, collecting tiny amounts of money from everyone with a job. Their goal is simple: the money you give them while you work is held for safekeeping and will be used to pay your pension when you retire. While this may seem simple on the surface, we have to wonder how these funds stay afloat in a cut-throat industry with its fair share of prolific failures. This begs the question: how do pension funds manage your money?

Put on your wetsuit, strap on your oxygen tank, and prepare to dive into the wonderful world of pensions, portfolios, and Pareto.

Historical financial markets

The Dutch love to boast that Amsterdam is the birthplace of financial markets as we know them today. Often, this story is immediately followed by the far less known story about how tulip bulbs also caused the first financial crash. However, the modern trillion-dollar financial industry likely traces its roots back further than this Dutch claim, all the way to 1300s Venice [1]. In this bustling heart of commerce on the Mediterranean coast, early brokers bought and sold debts, the predecessors of our modern-day bonds.

300 years later, the exploitation of the countries in what was then known as East India kickstarted the creation of the first stock market. In The Netherlands, England, and France, wealthy investors financed voyages to the East for a share in the profits of any ship that returned successfully. This spawned decentralized stock markets in port cities. The investor’s shares in the voyage were printed on paper and formed the first stock-based investment portfolios. By investing in several voyages at the same time, the investors could limit their exposure to the risk that a voyage would not make it back home because the average return on their investment was likely high enough to cover the cost. The 1602 charter for the Dutch East India Company (VOC) birthed the oldest centralised stock exchange: the Amsterdam Stock Exchange [2].

Nowadays, anybody can buy stocks (sometimes still called “shares”) for a whole range of companies. Although 400 years have passed since the first stock market was founded, the fundamental idea is still the same. A stock gives the holder a claim to a portion of the profits of an enterprise and the right to cast their vote during shareholder meetings. Investors, both private and institutional, invest in collections of stocks, bonds, and other financial instruments in the hopes of generating a profit. These collections of collections are known as portfolios.

Modern portfolio theory

The method used to decide which financial instruments to include in a portfolio is known as Portfolio Theory. At the core of every investment decision is the trade-off between the potential returns of an investment and the risk of the investment losing value over time. In 1952, Harry Markowitz founded the Modern Portfolio Theory (MPT) by defining investment decisions as the trade-off between the expected return (μ) and the expected standard deviation of returns (σ) for a given portfolio. Over 70 years later, the Markowitz model is still the foundation for how we think about the financial market.

Suppose we have the example portfolios as shown in Table 1 (for this explanation, we don’t worry about how we find these candidates):

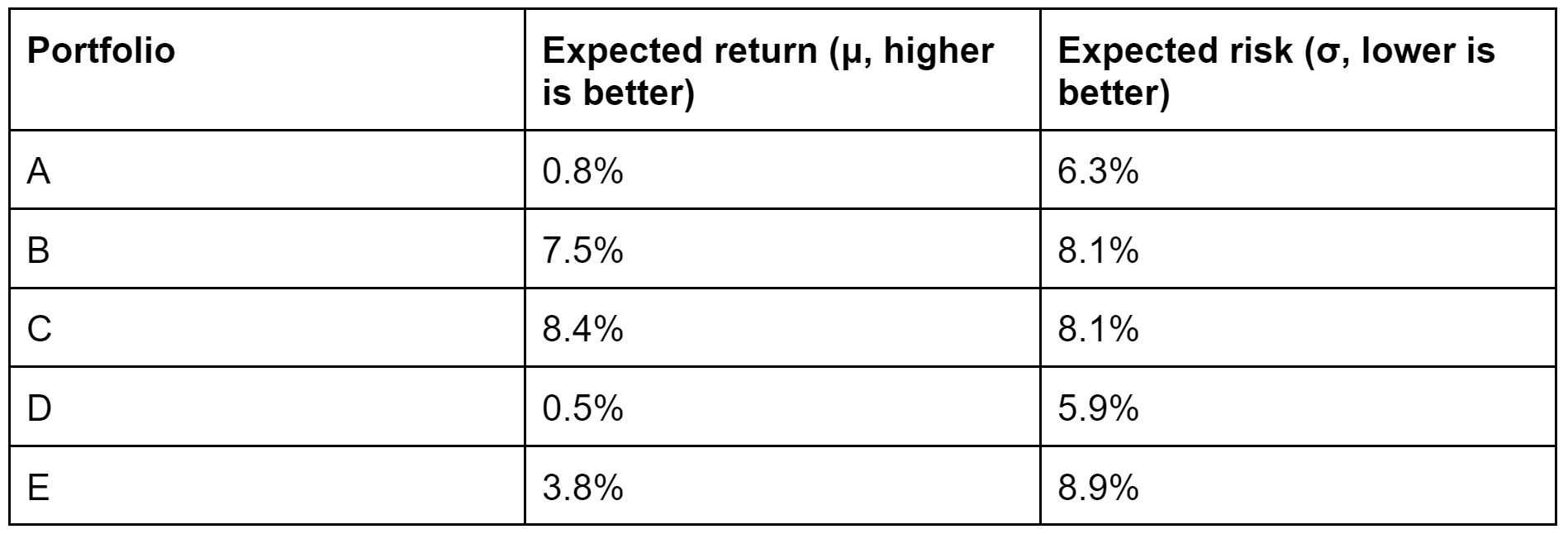
Assuming that these are the only possible portfolios, we now want to choose the portfolio that best fits our risk tolerance and also ensures that we are getting the best possible return. This makes some of the options in the table better than others. For example, portfolios B and E have a lower expected return and equal or higher expected risk compared to portfolio C. Therefore, a rational investor would never choose to invest in these portfolios unless they had some extra information not shown in the table.

Deciding between portfolios A, C, and D is not as simple. Each portfolio is better than the others in one of the performance metrics, but worse in the other. Portfolio D exposes an investor to the lowest expected risk and also generates the lowest expected return. An investor is given a trade-off decision: do I take more risk to have a chance at a higher return? This trade-off is the basis of the Pareto-dominance principle.

The Pareto principle states that given two options that are evaluated on multiple performance metrics (the expected return and expected risk in the case of our portfolios) two things may happen: one of the options is Pareto-dominant or the options are Pareto-indifferent. A dominant option is better in one or more metrics and at least equally as good in all other metrics. In our example, portfolio C is dominant compared to portfolios B and E. When the options are indifferent, neither option dominates. In our example, the portfolios A, B, and D are indifferent. Which of the indifferent portfolios is the most optimal depends on the risks that an investor is willing to take.

In a real-world scenario, investors can create a near-endless number of portfolios. Performing the work of finding all potential portfolios, comparing them against each other, and choosing one portfolio to invest in is impossible to do by hand. Therefore, modern investment firms use sophisticated algorithms to search for, evaluate, and choose the best portfolio for their risk profile. To protect their competitive advantage, these algorithms are not publicly available.

Luckily, access to the internet enables anyone to apply the Modern Portfolio Theory to their investment decisions. The principles, algorithms, and market information can be accessed with a laptop, access to the internet, and the right keywords. To get you started, these are some resources you could use as a starting point for your very own deep dive into the wonderful, wild world of investments: a history of multi-criteria decision-making [3], one method to find or create portfolios [4], navigating search spaces effectively [5], and an example approach to portfolio optimization [6].

With this article, you are one step closer to understanding the wondrous mathematics that governs the choices made by pension funds the world over. So far, we have only scratched the surface of what is possible in the financial markets. To discover the rest is up to you. Happy investing!

References

[1] Investopedia. ‘The Birth of Stock Exchanges’. Accessed 16 November 2023. https://www.investopedia.com/articles/07/stock-exchange-history.asp.
[2] Braudel, Fernand. Civilization and Capitalism, 15th-18th Century. New York: Harper & Row, Publishers, 1986.
[3] Köksalan, Murat, Jyrki Wallenius, and Stanley Zionts. 2016. ‘An Early History of Multiple Criteria Decision Making’. In Multiple Criteria Decision Analysis: State of the Art Surveys, edited by Salvatore Greco, Matthias Ehrgott, and José Rui Figueira, 3–17. International Series in Operations Research & Management Science. New York, NY: Springer. https://doi.org/10.1007/978-1-4939-3094-4_1.
[4] Agrrawal, P. 2013. ‘Using Index ETFs for Multi-Asset Class Investing: Shifting the Efficient Frontier Up’. The Journal of Index Investing 4 (2): 83–94.
[5] Emmerich, Michael T. M., and André H. Deutz. 2018. ‘A Tutorial on Multiobjective Optimization: Fundamentals and Evolutionary Methods’. Natural Computing 17 (3): 585–609. https://doi.org/10.1007/s11047-018-9685-y.
[6] Lwin, Khin T., Rong Qu, and Bart L. MacCarthy. 2017. ‘Mean-VaR Portfolio Optimization: A Nonparametric Approach’. European Journal of Operational Research 260 (2): 751–66. https://doi.org/10.1016/j.ejor.2017.01.005.